Develop spatial imagination
0.00 $
0 item(s)
Platonic solids. Platonic polyhedra. How to make pdf template
This group of five geometric solids was given the name of the ancient Greek scientist Plato. Mathematicians call these five polyhedra regular, but we most often call them the Platonic solids in ordinary speech.
First, let us identify these five geometric objects — or, in the terminology of mathematicians, geometric solids.
tetrahedron
octahedron
cube(hexahedron)
dodecahedron
icosahedronFirst of all, why are these five geometric solids called regular polyhedra?
This is quite easy to remember. The sides of regular polyhedra are regular polygons. In turn, regular polygons are those in which all sides are equal (e.g., triangle, square) and have equal angles between adjacent sides. This is why they are called "regular".
What is the connection with Plato?
The ancient Greek scientist Plato was most likely not related to discovering these remarkable polyhedrons, but Plato had another talent. In the modern world, Plato could be called the popularizer of regular polyhedra. The greatest contribution Plato made is that he told people about the existence of regular polyhedra.
If this is all he had done, however, the majority would have quickly forgotten about them. But Plato endowed these seemingly simple objects with incredible strength and mystical meaning and brought them to the forefront of his teaching.
In an attempt to explain the nature of everything that exists, Plato considered five regular polyhedra to be fundamental principles for the structure of each of the elements:
- fire correlated with the tetrahedron;
- air correlated with the octahedron;
- earth correlated with the hexahedron;
- water correlated with icosahedron;
- and the dodecahedron corresponded to the Universe.
It was the power of Plato's philosophy and mystical postulates that were entrenched in ordinary people's minds, which inextricably linked by these polyhedra with Plato's ideas. And, at some point, people began to talk about five regular polyhedra as Platonic solids.
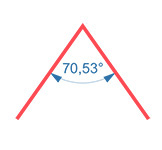
Three triangular faces converges at the same vertex of the tetrahedron. The three-dimensional angle between the three faces (solid angle of a tetrahedron at the vertex) is Ω = 0,55.
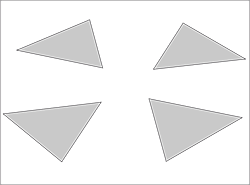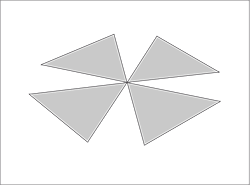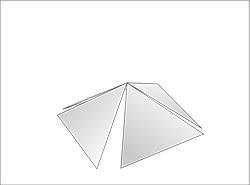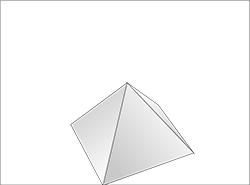Four triangular faces converges at the same vertex of the octahedron. The three-dimensional angle between the four faces (solid angle of an octahedron at the vertex) is Ω = 1,36.
Three quadrangles faces converges at the same vertex of the cube. The three-dimensional angle between the three faces (solid angle of a cube at the vertex) is Ω = 1,57.
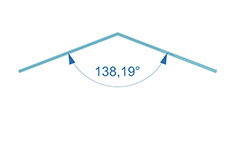
Five triangular faces converges at the same vertex of the icosahedron. The three-dimensional angle between the five faces (solid angle of an icosahedron at the vertex) is Ω = 2,63.
Three pentagonal faces converges at the same vertex of the dodecahedron. The three-dimensional angle between the three faces (solid angle of a dodecahedron at the vertex) is Ω = 2,96.
Popular
This little "joke" task will keep your kids (students) busy for a while! What plastic tetrahedron*...
The Lighthouse of Alexandria, one of the Seven Wonders, was built in the 3d century BC in an...
A star is an image of divine idea and will; due to them, our Light and Universe were created and...
The founders of Mirny, located in the Arkhangelsk region, placed a polyhedron, the Great...
For a primeval man, fire once became a new form of social life. The night ceased to be an...
So far, we have actively used glue to assemble polyhedrons from the Magic Edges sets. Moreover, we...
