The unit cell of water is tetrahedra containing five H2O molecules connected by hydrogen bonds. Moreover, each of the water molecules in simple tetrahedra retains the ability to form hydrogen bonds. Their simple tetrahedra can be joined together by vertices, edges, or faces, forming various spatial structures.
The hexagonal (hexagonal) structure is when the six water molecules (tetrahedra) are combined into a ring of all the various structures in nature. This type of structure is characteristic of ice, snow, and meltwater.

The tetrahedron form also has methane (CH₄) molecules and an ammonia (NH₃) molecule.

In nature, there are objects with the symmetry of the icosahedron—for example, viruses.
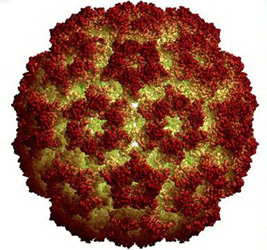
The exclusivity of the icosahedron was not accidental. It's all about saving - saving genetic information. You may ask: why is it necessarily the right polyhedron? And why exactly, icosahedron? The viral particle must turn the entire host cell metabolism upside down; it must force the infected cell to synthesize numerous enzymes and other molecules necessary to synthesize new virus particles. All of these enzymes must be encoded in viral nucleic acid. But its quantity is limited. Therefore, very little space is left to code its own membrane proteins in the virus nucleic acid. What does the virus do? It simply uses the same nucleic acid site many times to synthesize a large number of standard molecules — building proteins — that unite in the process of automating a virus particle.
The result is the maximum savings of genetic information.

According to mathematics laws, it remains to add that to construct the most economical way of a closed shell of identical elements, it is necessary to fold the icosahedron from them, which we observe in viruses.
Viruses solve by the most complicated task(it is called the "izopyrannoy"): finding the smallest surface body for a given volume and consisting of the same and the simplest figures. Viruses, the smallest of organisms, so simple that it is still not clear - refer them to living or inanimate nature - these same viruses have coped with the geometric problem that has required people for more than two thousand years! All the so-called "spherical viruses", including the poliovirus, are icosahedra, not a sphere, as previously thought.

Bacteriophages(Greek. Phagos - eater; literally - bacteria eaters) - bacterial viruses destroy bacteria and other microorganisms. Particles consist of a hexagonal or rod-shaped head with a 45–140 nm diameter and a 10–40 thick and 100–200 nm long. The bacteriophage is attached by its appendix to the bacterial cell and, secreting the enzyme, dissolves the cell wall; then, the contents of its head, through the Canadian process, pass into the cell, where the synthesis of bacterial proteins stops under the influence of the phage nucleic acid.