

Develop spatial imagination
0.00 $
0 item(s)
Hexahedron (Cube). How to make pdf template
The ancient Greeks gave the polyhedron a name by the number of faces. “Hexa” means six, “hedra” means a face (Hexahedron is a body with six faces).
Therefore, to the question “what is a hexahedron?”, We can give the following definition: “A hexahedron is a geometric solid of six faces, each of which is a regular quadrilateral (square)”.
The polyhedron belongs to regular polyhedra and is one of the five Platonic solids.
 The face of a polyhedron is a square. Each of the four angles is 90 degrees.
The face of a polyhedron is a square. Each of the four angles is 90 degrees.
Popular
Stamps cover all significant events happening in the world. Much attention was paid to polyhedra by...
The new Atom Browser creators decided to choose the image of a polyhedron or an icosahedron for...
This article will tell whether the “Magic Edges” can be attributed to a variety of origami. As the same...
Metal processing is a very complex process. But some masters can cut out polyhedrons from metal...
The box geometric shape from a distance resembles a rounded shape, emphasizing the similarity with the...
So far, we have actively used glue to assemble polyhedrons from the Magic Edges sets. Moreover, we...
When we demonstrate polyhedra assembled from the Magic Edges set, people often ask the same question...


 Total number of faces - 6
Total number of faces - 6


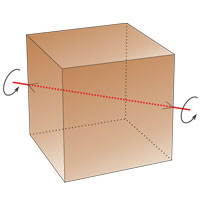
 Each edge (red) has three parallel edges (blue).
Each edge (red) has three parallel edges (blue).








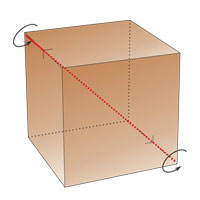
 The cube has a center of symmetry.
The cube has a center of symmetry.















 A cube can be placed in a sphere (inscribed) so that each of its vertices will touch the sphere's inner wall.
A cube can be placed in a sphere (inscribed) so that each of its vertices will touch the sphere's inner wall.













