Develop spatial imagination

0.00 $
0 item(s)

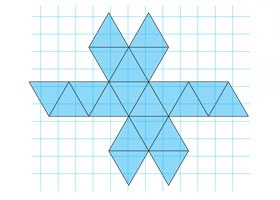
Icosahedron. How to make pdf template

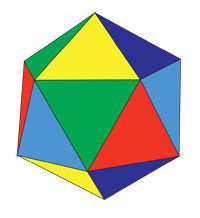
The ancient Greeks gave the polyhedron a name according to the number of faces. “Ikosi” means twenty, “hedra” means a face (Icosahedron is solid with twenty faces).

Therefore, the question “What is an icosahedron?” The following definition can be given: “An icosahedron is a geometric solid of twenty faces, each of which is a right triangle.”

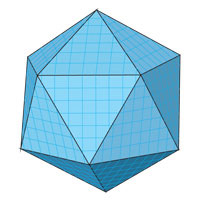
The polyhedron belongs to regular polyhedra and is one of the five Platonic solids.
The icosahedron has the following characteristics:

The face type is a regular triangle;
The number of sides at the verge 3;
The total number of faces is 20;
The number of edges adjacent to the top is 5;
The total number of vertices is 12;
The total number of edges is 30.

The regular icosahedron is composed of twenty equilateral triangles. Each vertex of an icosahedron is a vertex of five triangles. Therefore, each vertex's sum of flat angles is 300° (60° * 5).
The icosahedron has a center of symmetry - the center of the icosahedron has 15 axes of symmetry and 15 planes.

Mathematical characteristics of icosahedron

An icosahedron can be placed in a sphere (inscribed) so that each of its vertices will touch the inner wall of the sphere.

The radius of the described sphere of the icosahedron

Where "a" - is the side length.

The sphere can be inscribed inside the icosahedron.

The radius of the icosahedron inscribed sphere

The surface area of an icosahedron can be represented as a shape net area.
The icosahedron surface area can be defined as the area of one of the icosahedron's sides. This is the area of a regular triangle, multiplied by 20. Or use the formula:

The following formula determines the volume of the icosahedron:

Icosahedron shape nets

You can make an icosahedron by yourself. Paper or cardboard is the most suitable option. You will need a paper net for assembly, a single sheet with lines for all the folds.

Plato

Choose a color for your polyhedron.

The ancient Greek philosopher, Plato, associated the icosahedron with the "earth" element - water. Therefore, to build a model of this regular polyhedron, we chose blue.

The figure shows an icosahedron net:

Note that this is not the only option for an icosahedron net.

To build a model, you can download a net in pdf format and print it on an A4 sheet:
- if you print on a color printer - color net.
- if you intend to use colored cardboard for the assembly - standard net.

Also, there are two classic versions of color for the polyhedron, when each of the adjacent faces is painted in its own color. The same colors do not border with each other.

We present two options for painting 20 faces of the icosahedron using five colors.

icosahedron five colors

The first variant of the icosahedron coloring implies that every five vertexes will have all five colors.

Download net:

icosahedron five colors

The second variant of the coloring of the icosahedron provides the opposite faces of the same color.

Download net:

Icosahedron from the "Magic Edges" set

Video. The rotation of all regular polyhedra

Icosahedron. How to make pdf template

Therefore, the question “What is an icosahedron?” The following definition can be given: “An icosahedron is a geometric solid of twenty faces, each of which is a right triangle.”

Mathematical characteristics of icosahedron

Popular