Develop spatial imagination
0.00 $
0 item(s)
Dual pairs of polyhedra
What do the dodecahedron and icosahedron have in common?
These two polyhedra have the following fundamental parameters:
|
The form of each side |
Pentagon |
Triangle |
|
Number of sides |
12 |
20 |
|
Number of vertices |
20 |
12 |
If we pay attention to the number of sides and vertices of these two polyhedra, they are the opposite.
What does this mean for us? Based on a dodecahedron, an icosahedron can be constructed.
To do this, on each of the 12 faces of the dodecahedron, we select the face center. By connecting all the centers, we obtain an icosahedron. This obtained icosahedron will be exactly inscribed in the original dodecahedron.
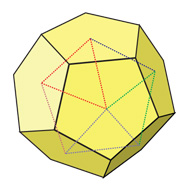
A similar procedure can be performed on an icosahedron and obtained from it a dodecahedron.
This property indicates that the icosahedron and the dodecahedron form a dual pair.
Video from our partners - the team "ART KOSEKOMA", clearly demonstrates this transformation.
An interesting feature in the transition from a dodecahedron to an icosahedron is the emergence of three polyhedra belonging to the class of semi-regular words, in other words, Archimedean solids.
Popular
Sometimes you hear the question: “Why did you choose paper (or more precisely, design cardboard) to...
The perfection of the spherical shape has long attracted thinkers and scientists who, using...
It is round, but nobody canceled the shape net of parts for its...
A polyhedronis a solid bounded by flat polygons, which are called faces....
Summer is the time you want to spend outdoors. At the desk, the children will sit down in...
Architects have used the elements of polyhedra in designing their constructions since ancient...
The “business card” of the Republic of Belarus is a new building of the National Library in Minsk....
