There is a concept that a polyhedron's vertex gives off energy, and the plane absorbs energy. In that case, if there are more vertices in the polyhedron than planes, then it has the energy "Yan". In the opposite case, the energy is "Yin."

To begin with, remember what is "Yin" and "Yang". It is believed that in China, the words "Yin" and "Yang" meant "shadowed" and "lit" mountain slopes.
The simplicity and, at the same time, the depth of this idea of ​​Chinese philosophers are amazing. Firstly, the mountain is always a single unit consisting of both slopes. Secondly, the lighting of the mountain changes during the day, as the Earth rotates relative to the Sun. And that slope, which was first light, then becomes dark and vice versa. It turns out that all the opposites are parts of a single whole and interconnected, interact and interpenetrate.
Discovered in China several millennia ago, this principle was originally based on physical thinking. The one primordial matter gives rise to two opposite substances - "Yang" and "Yin", which are one and indivisible. "Yin" meant "northern, shadow", and "Yang" - "southern, sunny slope of the mountain." Later, "Yin" was perceived as negative, cold, dark, feminine, and "Yang" - as positive, bright, warm, and masculine.
The symbol of the creative unity of opposites in the Universe was depicted as a circle, an image of infinity, divided by a wavy line into two halves - dark and light. Two points symmetrically located inside the circle — light on a dark background and dark on a light — indicated that each of the two great forces of the Universe carries within itself a germ of the opposite origin.

The tetrahedron has four vertices and four faces, which leads to the Yin – Yang equality.

The octahedron has six points-vertices of radiation and eight points-centers of absorption faces. Consequently, the octahedron absorbs more energy than it radiates, so it belongs to the female "Yin" principle.

The hexahedron (cube) has 8 vertex points radiating energy and six faces at which energy is absorbed. Since there are more emitting points than absorbing ones, the cube belongs to Yang's male principle.

The dodecahedron has 20 vertices and 12 faces, and therefore it expresses the principle of "Yang."

The icosahedron has 12 vertices and 20 faces that look like regular triangles, so it expresses the principle of "Yin."

It should be noted that the radiative centers can be placed at the centers of the faces and the absorption centers at the vertices. Obviously, this will lead to an inversion of relations (Yin-Yang), which confirms the unity and opposite of these two principles.

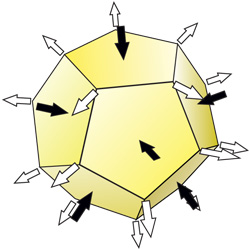
And now the question! What type of energy does the polyhedron belong to - the Great Stellated Dodecahedron?
Yin-Yang?

 

(send your decisions to This email address is being protected from spambots. You need JavaScript enabled to view it.)
© polyhedr.com 29/04/2014