When Euler's Formula for Polyhedra Doesn't Work

Euler’s Formula for polyhedra is a remarkable mathematical formula connecting the number of vertices, edges, and faces of a polyhedron.

The formula states:

V−E+F=2

where:
V — number of vertices;
E — number of edges;
F — number of faces of the polyhedron.

One can think of Euler’s Formula as a magical rule, helping us understand whether a polyhedron can be constructed with a certain number of vertices, edges, and faces. If we add the number of vertices and faces, and then subtract the number of edges, and if we get 2, then it's correct!

Let’s consider how this formula works using a cube as an example.

Number of Vertices and Edges of a Cube
A cube has: 8 vertices, 12 edges, and 6 faces.

Let’s plug these values into Euler’s formula:

8−12+6=2
2=2

Thus, Euler's Formula confirms that a cube is a valid polyhedron as the values substitute correctly into the equation.

Let’s take on a more complex challenge.
We made two holes in a cube, directly opposite each other. These holes are also cubic in shape, only smaller (2/3 of the main cube).
Let’s see what we got.

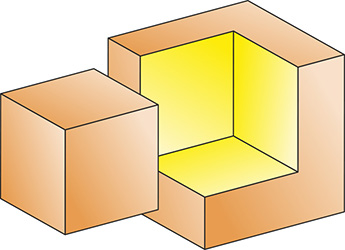
We’re not merely looking at a cube! This is something similar to a ring. In mathematics, such a shape is referred to as a toroid. You might have heard of toroids as fascinating geometric figures, such as the Szilassi polyhedron discovered by Hungarian mathematician Lajos Szilassi.

Task!
Try calculating the number of vertices, edges, and faces for this polyhedron and substitute them into Euler’s formula.
V−E+F=?
Find the solution.

For visual understanding, we suggest assembling a model of such a polyhedron from cardboard. You can download the layout for assembling the cube with an edge length of 66mm here:

To assemble our model, we will compile it from three parts!
First Step: Take the first part and connect it to form a ring!

Second Step: Now glue the second part to our ring.

Third Step: And the final step! Attach the third part.

We obtain a toroid based on a cube.

Solution to the Problem:
To count the number of faces, it’s easiest to use the layout of our model. We count the colored faces. There will be 12. The number of vertices can be counted in the picture:

To keep count, we recount the edges first parallel to one side, then parallel to the second and third:

Our new polyhedron has: 24 vertices, 36 edges, and 12 faces.

We substitute the values into Euler’s formula
24−36+12=0

We get a value of 0, not 2 as in the original form of the formula.

Why?

The Euler's Formula we discussed earlier applies to convex polyhedra, such as cubes or pyramids, and it is not directly applicable to more complex surfaces, such as toroids.

However, for topological objects like a toroid, there is a more generalized version of Euler’s formula, which also considers the number of connected components and the number of "holes" in the surface:

V−E+F=2−2g

Here:
V - number of vertices
E - number of edges
F - number of faces
g - genus of the surface (number of "holes")

For a toroid, which has one "hole" (i.e., the toroid is a genus 1 surface), the formula becomes:

V−E+F=2−2⋅1=0

Thus, for a toroid, the number of vertices minus the number of edges plus the number of faces equals zero. This generalization of Euler's formula helps mathematicians explore diverse and complicated shapes, beyond simple polyhedra.

© polyhedr.com 29/09/2023