Spatial Cross

An example of what can be assembled from cubes.

We took 8 shape nets of cubes from the 12th issue of "Magic Edges".

By gluing together 5 cubes, one can achieve a cross-shaped figure resembling a pharmacy's street advertisement.

Add two more cubes, and we get a figure with its own unique name – the "spatial cross". The spatial cross is a 3D geometric figure representing the shape of a cross in any projection.

And if you add one more cube to the bottom, as Salvador Dali did in his painting, you get a geometric solid – the "tesseract shape net".

To start, what is a tesseract? A tesseract is a cube in four-dimensional space. The usual cube, which we can imagine, exists in three-dimensional space. It has length, height, and width. But try to assume that there exists a space with an additional dimension beyond the aforementioned ones. Understanding this isn't simple. However, researchers have agreed on what the image of a hypercube (tesseract) will look like:

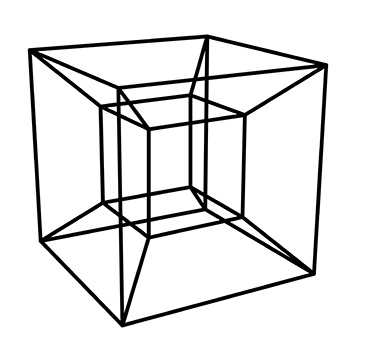
They even devised a way to transition from this image to the tesseract shape net in three-dimensional space. An animated video was taken from Wikipedia pages:

Salvador Dali's painting "Corpus Hypercubus". The 1954 painting depicts Jesus Christ crucified on the hypercube shape net (tesseract).

The distinct similarity of the hypercube to crucifixion led to the emergence of the most unusual portrayal of the crucified Jesus in art history. It also became a remarkably talented example of the symbiosis of science and religion in a work of art. Dali's interest in not only the hypercube but also the fourth dimension was not accidental. The fact is that thoughts of death, which increasingly troubled Dali from a certain point, did not inspire the artist at all. On the contrary: he considered the very possibility of his own death extremely foolish - and therefore intended to avoid transformation into inanimate matter by all means. Among them, he believed the transition to the fourth dimension, which, according to Dali himself, offers true immortality, to be the most reliable. A photograph of the famous artist – surrealist with a model of the tesseract shape net.

© polyhedr.com 23/10/2023