Develop spatial imagination
0.00 $
0 item(s)
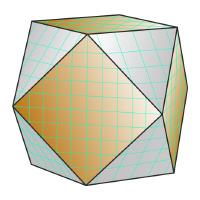
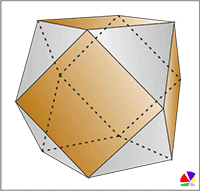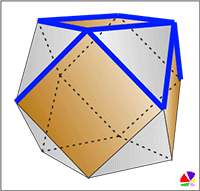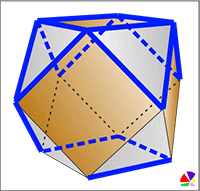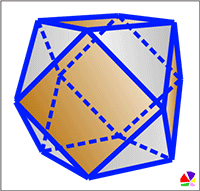
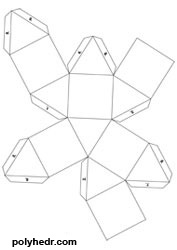
Cuboctahedron. How to make pdf template
This polyhedron is obtained by successively cutting off each of the vertices of the octahedron or cube.
A cuboctahedron is a semiregular convex polyhedron with two properties:
1. All faces are regular polygons of two types, a triangle, and a square;
2. For any pair of vertices, there is a symmetry of the polyhedron (that is, a motion that translates the polyhedron into itself) that transforms one vertex to another.
The cuboctahedron is one of the 13 solids of Archimedes.
Archimedean solids are semiregular polyhedra in the sense that their faces are regular non-similar polygons. Simultaneously, the condition of one of the types of spatial symmetry (tetrahedral, octahedral, or icosahedral) is preserved.
Popular
A polyhedronis a solid bounded by flat polygons, which are called faces....
Can a polyhedron be curved? Perhaps this is some mistake? Or maybe this is not a polyhedron? It...
Euler’s Formula for polyhedra is a remarkable mathematical formula connecting the number of...
The Great Archimedes is ready to help us. And it's great! According to legends, Archimedes created...
Under the guidance of Tatyana Yurievna Timofeyeva, a teacher of mathematics, the guys worked on the...