As a cover for this article, we offer a picture from a popular TV show.

So the question.

Cutting the cube into two equal halves, we get a cross-section ...?

- A: square;

- B: rectangle;

- C: rhombus;

- D: hexagon.

If you think the answer A (square) is obvious and discard all other answers, then you are making a big mistake. It may seem that, for example, such an answer as D: (hexagon) is obviously superfluous here. But this is not the case. All answers are correct here!

This article is inspired by the popular Fruit ninja game where it is necessary to cut the flying fruit with a sword. Let's say that the majority of fruits are round or oval. When cutting such fruits into halves, pay attention to what will be in the place of the cut. What is the geometric shape? If we cut accurately and quickly, then there will be a section in the shape of a circle or an oval.

How do you like the proposal to cut a classic cube? Here you will have to think.

But we will complicate the task even more. The task is to cut the cube in such a way that after the cut, equal halves are obtained.

How can you demonstrate that this is possible? How can you prove that a cube can be cut into two equal halves?

To do this, we will consider each answer and make cube models consisting of two halves.

We will use a shape net of only one half. To eliminate all doubts.

But what about the other half?

The second half should be exactly the same as the first. Then the statement will be proved.

Just reassemble the half from the same shape net.

Put the halves together and you have the original cube!

Cube Cross-section - Square

The square cross-section of the cube can be obtained in different ways (2, 3). But to get a square section with the condition that the two halves are equal, there is only one single way (1).

We will make a paper cube. The dimensions of the cube are determined by the side length, we choose 70 mm.

It will be convenient to place such a shape net on a standard A4 sheet. The model of a cube with a 70 mm long side will be very comfortable to hold in your hands.

We need:

• - two sheets of A4 paper;
• - scissors;
• - glue.

Download cube shape net

1. Print the shape net twice.

2. Carefully cut the shape net along the outline.

3. Bend the flaps at the folds.

4. Glue the flaps in the sequence shown.

5. For clarity, you can connect the two halves of the cube with adhesive tape.

So, the first proof is received!

The cube can be cut into two equal halves with a cross-section in the shape of a square.

Cube Cross-section - Rectangular

A rectangular section, a cube can also be obtained in different ways (2, 3). And all of these options will be correct. Since both conditions are met:

- cross-section - rectangle;

- the cube is divided into two identical halves.

For our model, we choose an option that has a cross-sectional rectangle with a maximum area (1).

We will make a paper cube.

We need:

• - two sheets of A4 paper;
• - scissors;
• - glue.

Download cube shape net

1. Print the shape net twice.

2. Carefully cut the shape net along the outline.

3. Bend the flaps at the folds.

4. Glue the flaps in the sequence shown.

5. For clarity, you can connect the two halves of the cube with adhesive tape.

So, the second proof is received!

Cube Cross-section - Rhombus

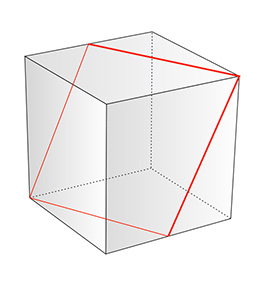
The cube rhombus cross-section can be obtained in one and only way.

We will make a paper cube.

We need:

• - two sheets of A4 paper;
• - scissors;
• - glue.

Download cube shape net

1. Print the shape net twice.

2. Carefully cut the shape net along the outline.

3. Bend the flaps at the folds.

4. Glue the flaps in the sequence shown.

5. For clarity, you can connect the two halves of the cube with adhesive tape.

So, the third proof is received!

The cube can be cut into two equal halves with a cross-section rhombus.

Cube Cross-section - Regular Hexagon

By cutting the cube into two equal halves, we can obtain both a non-regular hexagon cross-section (2) and a regular hexagon cross-section (1). The inclination of the section plane relative to the selected axis of symmetry allows you to make the necessary section. The extreme slope of the plane creates a cross-section - rhombus (3).

For our model, we choose the option with a cross-section in the form of a regular hexagon.

We will make a paper cube.

We need:

• - two sheets of A4 paper;
• - scissors;
• - glue.

Download cube shape net

1. Print the shape net twice.

2. Carefully cut the shape net along the outline.

3. Bend the flaps at the folds.

4. Glue the flaps in the sequence shown.

5. For clarity, you can connect the two halves of the cube with adhesive tape.

So, the fourth proof is received!

The cube can be cut into two equal halves with a cross-section, in the form of a regular hexagon.

What conclusion can be drawn from this article?

Sometimes it is quite difficult for our imagination to imagine operations with volumetric bodies. But if we twirl the object in our hands, the situation becomes clearer.

Learn more about cross-sections of geometric solids here.

© polyhedr.com 05/17/2021